yoo-s.com

RuntimeException No application encryption key has been specified

Laravel 2019/05/02

プロジェクトを整理していたら、アプリケーションキー「encryption key」を消失http://xxx.xxx.xxx.xxx:8000/ のアクセス時に Runtimeエラーが表示作成する

$ php artisan key:generate
Application key set successfully.

実際にはクラスファイル「KeyGenerateCommand」で、Laravel Config設定に基づき、 base64_encode() と Encrypter::generateKey() でランダムキーを生成している模様。 Illuminate Foundation Console KeyGenerateCommand

    public function handle()
    {
        $key = $this->generateRandomKey();
       .....
        $this->laravel['config']['app.key'] = $key;
    }
    protected function generateRandomKey()
    {
        return 'base64:'.base64_encode(
            Encrypter::generateKey($this->laravel['config']['app.cipher'])
        );
    }

Linux PHPパッケージの用意

通常PHP環境（PDO, JSON, LAMP & LAPP...）で最低限入れておけば動作しそうだが、laravel プロジェクト作成のバージョンによって異なる Installation(5.8)

# aptitude install php-zip php7.3-pdo php7.3-pgsql php7.3-mysql php7.3-mbstring php7.3-ssh2 php7.3-gd php7.3-curl php7.3-tokenizer php7.3-bcmath php7.3-ctype

composer の用意

PHP7.3 で環境を作成するため、ソースでインストールした。（Debian9系パッケージの composer だとエラーになる） PHP7.3 で compser install できない

composer -V
Composer version 1.8.5

Laravel インストール & プロジェクト作成

composer で Laravel をインストールし、~/.config/composer/vendor/ にコマンドパスを通す

$ composer global require "laravel/installer"
$ export PATH="~/.config/composer/vendor/bin:$PATH"

プロジェクト作成（laravelコマンド）

この時点でエラーになる場合は、ライブラリが不足している可能性があるライブラリが膨大なため、まぁまぁ時間がかかる

$ laravel new project_name
...
  - Installing symfony/translation (v4.2.7): Downloading (100%)         
  - Installing nesbot/carbon (2.17.1): Downloading (100%)         
  - Installing monolog/monolog (1.24.0): Downloading (100%)         
  - Installing league/flysystem (1.0.51): Downloading (100%)         
  - Installing laravel/framework (v5.8.14): Downloading (100%)  
...
Package manifest generated successfully.
Application ready! Build something amazing.

パーミッション変更

storage, bootstrap/cache のパーミッションを変更しないと起動できない

$ chmod -R 777 storage
$ chmod -R 777 bootstrap/cache

ここら辺はコマンド自動化した方が良いかと

プロジェクト作成（Composerコマンド）

こちらの方が一般的か？ laravel のパスが利用できない場合は、以下のコマンドで作成

$ composer create-project laravel/laravel --prefer-dist project_name 5.8

Laravelサーバ起動

個人環境では、Mac上にVirtualBox（Debian）サーバを別IPでルーティングしているため、IPの指定（--host）が必要

$ php artisan serve --host=192.168.11.56

Laravel

リダイレクト設定

artisan serve でなく Apache で動作させる場合、public のリダイレクト設定が必要 VirtualHost で設定する方法もあるが、「.htaccess」で public をルートとみなすようにする

PHP7.x & Laravel5.x

    
        Options -MultiViews
    

    RewriteEngine On

    RewriteCond %{REQUEST_FILENAME} -d [OR]
    RewriteCond %{REQUEST_FILENAME} -f
    RewriteRule ^ ^$1 [N]

    RewriteCond %{REQUEST_URI} (\.\w+$) [NC]
    RewriteRule ^(.*)$ public/$1

    RewriteCond %{REQUEST_FILENAME} !-d
    RewriteCond %{REQUEST_FILENAME} !-f
    RewriteRule ^ server.php

PHP7.3 で compser install できない

PHP 2019/04/29

PHP7.3 で break と continue の取り扱いが変更になった影響で、composer install がエラーになる場合、

PHP7.2にさげる
composer のバージョンをあげる

ul>

$ composer global require "laravel/installer"
Changed current directory to /home/yoo/.config/composer
Using version ^2.0 for laravel/installer
./composer.json has been created
Loading composer repositories with package information
Updating dependencies (including require-dev)

Installation failed, deleting ./composer.json.
                                                                                           
  [ErrorException]                                                                         
  "continue" targeting switch is equivalent to "break". Did you mean to use "continue 2"?  
                                                                                           
require [--dev] [--prefer-source] [--prefer-dist] [--no-progress] [--no-update] [--no-scripts] [--update-no-dev] [--update-with-dependencies] [--ignore-platform-reqs] [--prefer-stable] [--prefer-lowest] [--sort-packages] [-o|--optimize-autoloader] [-a|--classmap-authoritative] [--] []...

特に初期設定で composer のバージョンが低い場合は注意が必要（composer self-udpate がないなど） composer installができなくなった時の解決法（PHP7.3）

PHP7.2 に変更

$ sudo update-alternatives --config php
  選択肢    パス           優先度  状態
------------------------------------------------------------
*0            /usr/bin/php7.3   73        自動モード
  1            /usr/bin/php5     50        手動モード
  2            /usr/bin/php7.0   70        手動モード
  3            /usr/bin/php7.2   72        手動モード
  4            /usr/bin/php7.3   73        手動モード

composerの再インストール（self-udpateなど利用できない場合）

composer-setup.php をダウンロード・実行する

$ curl -sS https://getcomposer.org/installer | php
$ sudo php composer-setup.php --install-dir=/usr/local/bin --filename=composer
$ composer -V
Composer version 1.8.5 2019-04-09 17:46:47

2019/12/09追記一発でインストールする

$ curl -s https://getcomposer.org/installer | php && sudo mv -v composer.phar /usr/local/bin/composer

配列結合 array_merge() と演算子の違い

PHP 2019/04/25

PHPの配列は他の言語と比べて若干癖がある。インデックスが型が整数か文字列とか連番でなくてもよいとかゆるいので、ある意味柔軟なデータを生成する事もできる。（ここら辺は言語思想）

PHP配列の結合は「array_merge() 」が一般的かも知れないが、演算子でも計算できる。ただし、インデックスによって結果が異なるので注意が必要。

インデックスが同じ、異なる
値が同じ、異なる

の組み合わせで考察してみる。

事前に結合するサンプルデータを作成しておく（例では10個ずつ）。

    function generateValues($count, $prefix = 'test', $from_index = 1)
    {
        for ($i = $from_index; $i <= $count + $from_index; $i++) $values[$i] = "{$prefix}{$i}";
        return $values;
    }

$values1 = 
array (
  0 => 'test0',
  1 => 'test1',
  2 => 'test2',
  3 => 'test3',
  4 => 'test4',
  5 => 'test5',
  6 => 'test6',
  7 => 'test7',
  8 => 'test8',
  9 => 'test9',
)
$values2 = 
array (
  0 => 'test0',
  1 => 'test1',
  2 => 'test2',
  3 => 'test3',
  4 => 'test4',
  5 => 'test5',
  6 => 'test6',
  7 => 'test7',
  8 => 'test8',
  9 => 'test9',
)

$values1 + $values2 の結合（インデックス同じ、値同じ）

$values1 + $values2 を演算子「+」で結合してみる。

//values1 + values2
$values1 = $array_merge->generateValues(10);
$values2 = $array_merge->generateValues(10);
$values = $values1 + $values2;

$values1 + $values2 = 
array (
  0 => 'test0',
  1 => 'test1',
  2 => 'test2',
  3 => 'test3',
  4 => 'test4',
  5 => 'test5',
  6 => 'test6',
  7 => 'test7',
  8 => 'test8',
  9 => 'test9',
)

インデックスが同じだと結合できない。またどちらの配列が採用されているかわからないので、値の違う配列を作成して調べる。

$values1 + $values2 の結合（インデックス同じ、値異なる）

//values1 + values2
$values1 = $array_merge->generateValues(10, 'red');
$values2 = $array_merge->generateValues(10, 'blue');
$values = $values1 + $values2;

$values1 = 
array (
  0 => 'red0',
  1 => 'red1',
  2 => 'red2',
  3 => 'red3',
  4 => 'red4',
  5 => 'red5',
  6 => 'red6',
  7 => 'red7',
  8 => 'red8',
  9 => 'red9',
)
$values2 = 
array (
  0 => 'blue0',
  1 => 'blue1',
  2 => 'blue2',
  3 => 'blue3',
  4 => 'blue4',
  5 => 'blue5',
  6 => 'blue6',
  7 => 'blue7',
  8 => 'blue8',
  9 => 'blue9',
)
$values1 + $values2 = 
array (
  0 => 'red0',
  1 => 'red1',
  2 => 'red2',
  3 => 'red3',
  4 => 'red4',
  5 => 'red5',
  6 => 'red6',
  7 => 'red7',
  8 => 'red8',
  9 => 'red9',
)

上書きされずに最初の配列が採用されていることがわかる。

array_merge($values1, $values2)での結合（インデックス同じ、値同じ）

同じ内容の配列を array_merge() するとインデックスが振り直された配列を返す。

$values = array_merge($values1, $values2);

array (
  0 => 'test0',
  1 => 'test1',
  2 => 'test2',
  3 => 'test3',
  4 => 'test4',
  5 => 'test5',
  6 => 'test6',
  7 => 'test7',
  8 => 'test8',
  9 => 'test9',
  10 => 'test0',
  11 => 'test1',
  12 => 'test2',
  13 => 'test3',
  14 => 'test4',
  15 => 'test5',
  16 => 'test6',
  17 => 'test7',
  18 => 'test8',
  19 => 'test9',
)

今度は、インデックスの異なる配列で試してみる。配列の作成は以下で作成

    function generateValuesWithIndex($count, $prefix = 'test')
    {
        for ($i = 0; $i < $count; $i++) {
            $values[$this->index++] = "{$prefix}{$i}";
        }
        return $values;
    }

$values1 = 
array (
  0 => 'test0',
  1 => 'test1',
  2 => 'test2',
  3 => 'test3',
  4 => 'test4',
  5 => 'test5',
  6 => 'test6',
  7 => 'test7',
  8 => 'test8',
  9 => 'test9',
)
$values2 = 
array (
  20 => 'test0',
  21 => 'test1',
  22 => 'test2',
  23 => 'test3',
  24 => 'test4',
  25 => 'test5',
  26 => 'test6',
  27 => 'test7',
  28 => 'test8',
  29 => 'test9',
)

$values1 + $values2 の結合（インデックス異なる、値同じ）

$values = $values1 + $values2;

$values1 + $values2 = 
array (
  0 => 'test0',
  1 => 'test1',
  2 => 'test2',
  3 => 'test3',
  4 => 'test4',
  5 => 'test5',
  6 => 'test6',
  7 => 'test7',
  8 => 'test8',
  9 => 'test9',
  20 => 'test0',
  21 => 'test1',
  22 => 'test2',
  23 => 'test3',
  24 => 'test4',
  25 => 'test5',
  26 => 'test6',
  27 => 'test7',
  28 => 'test8',
  29 => 'test9',
)

インデックスを保持したまま結合できる。

array_merge($values1, $values2)での結合（インデックス異なる、値同じ）

$values = array_merge($values1, $values2);

array (
  0 => 'test0',
  1 => 'test1',
  2 => 'test2',
  3 => 'test3',
  4 => 'test4',
  5 => 'test5',
  6 => 'test6',
  7 => 'test7',
  8 => 'test8',
  9 => 'test9',
  10 => 'test0',
  11 => 'test1',
  12 => 'test2',
  13 => 'test3',
  14 => 'test4',
  15 => 'test5',
  16 => 'test6',
  17 => 'test7',
  18 => 'test8',
  19 => 'test9',
)

インデックスが振り直されて結合される。

[Debian]PHPのaptパッケージが消失？

Linux 2019/03/26

upgrade などしてしまって、PHP7.2のパッケージが消失してしまう。

以下を参照 How To Install PHP (7.3, 7.2 & 5.6) on Debian 9 Stretch

PHP7.2を Debian 9（stretch）にインストールする方法

p class="code">$ sudo apt-get install apt-transport-https lsb-release ca-certificates $ sudo wget -O /etc/apt/trusted.gpg.d/php.gpg https://packages.sury.org/php/apt.gpg $ echo "deb https://packages.sury.org/php/ $(lsb_release -sc) main" | sudo tee /etc/apt/sources.list.d/php.list 認証して、/etc/apt/sources.list.d/ に php.list を新たに追加している模様

[脱jQuery]始める前に

JavaScript 2019/03/15

「脱jQuery」を始める前に

近年「脱jQuery」のワードが出ているが、手法を間違えると「jQuery」で良かったということにも・・・「jQueryのここが便利だったのか」と痛感することも結構あります。

何のために「脱jQuery」をするのか？目的が明確である

周りが発言しているからという曖昧な理由でなく、「脱jQuery」した未来予想図を作っておきます。（JavaScript、フレームワーク知識向上、半自動化などの開発効率化の目処など）特にJSフレームワークを利用しない場合、jQueryの部分を全て自分で書き直す覚悟が必要でしょう。

代用するJSフレームワークで開発・設計が確立している

「Vue.js」「AngularJS」「React」の選択肢が決まっていて、バックエンドやテンプレート管理の設計ができている。恐らく、これが今一番主流でしょう。ただしフレームワークや設計方法の理解度が低いと、プロジェクトが破綻する可能性がある。

自分でライブラリ・フレームワーク・設計が確立できる

「脱jQuery」をしたことで、ソース管理が余計に複雑になってしまう事が多々ある。特にjQuryライブラリに依存したプロジェクトを書き換えると相当な労力を要するので覚悟が必要である。

など、案件によってよく吟味して作業した方が良い。

「既存JSフレームワーク」を始める前に

現在は「Vue.js」「AngularJS」「React」が主流「YUI」「Backbone.js」などフェイドアウトしていくフレームワークも多々あるので、選択を間違えないようにネイティブの知識の保険をかける必要がある。

個人的なロードマップとして、既存JSフレームワーク利用の前に、自作フレームワークを作成してある程度経験を積み、同時に「Vue.js（個人的にイチオシ）」「AngularJS」の情報も蓄積しつつ、効率的・自動化を踏まえて移行するつもりだ。

過去の経験から既存JSフレームワークを安易に利用すると、

・知識が浅いと構造がグチャグチャになる・効率化するにはJSフレームワーク以外の設計知識も必要・進化が早いので、圧倒的な仕様変更に対応できない

になるためだ。

現在（2019/03時点）は「ECMAscript 6」が主流であるので、「ECMAscript 7」は必要な時に利用していく。更に「TypeScript」を併用するのが理想かもしれないが、まずはネイティブの知識を復習・蓄積していく。

個人的な目標

・JavaScriptネイティブ追求・Dom操作追求・MVC設計において他のフレームワークとの一般共通化・View（テンプレートエンジン）の手法・管理・バックエンドの親和性・開発半自動化

などを目標とします。

[VSCode]th td を自動整形させない

VSCode 2019/03/14

入れる機能拡張や設定によるが、テーブルの「td」「th」はデフォルトで自動整形は改行されてしまう。（div とかは改行されない・・・）


  都市


  東京

個人的に好きではないので、「td」「th」は改行しないように変更

VSCode「html.format」設定

「html.format.contentUnformatted」にタグをカンマ区切りで記述

"html.format.contentUnformatted": "th,td,pre,code,textarea",

都市
東京

ただし、予め改行されているものはこの設定だけでは１行にできない模様

VirtualBox6のMacマウント

Virtualbox 2019/02/06

2018年12月にVirtualBox6.0がリリースされたので、アップデートしたが共有フォルダのマウントも再構築しないといけない。基本的な設定方法は以下に記載 [Debian]Virtualbox(Debian)とmac(OS X)のフォルダ共有ここではLinux用の「VirtualBox6.0.0」を利用 ※2/6時点で最新版は6.0.4

Mac

Debian イメージの共有フォルダを debian というフォルダ名で有効

$ VBoxManage setextradata Debian VBoxInternal2/SharedFoldersEnableSymlinksCreate/debian 1

Linux

ダウンロードとインストール

# wget http://download.virtualbox.org/virtualbox/6.0.0/VBoxGuestAdditions_6.0.0_RC1.iso
# mount -r VBoxGuestAdditions_6.0.0_RC1.iso /media/cdrom
# sh /media/cdrom/VBoxLinuxAdditions.run

「/sbin/mount.vboxsf」は自動的に更新されていたようだ。

自動マウントエラー

以前はVirtualBox側で自動マウントでも動作していたが、Virtualbox6から（？）はプロトコルエラーになる。

/sbin/mount.vboxsf: mounting failed with the error: Protocol error

VirtualBox イメージ > 設定 > 共有フォルダ > 自動マウントのチェックを外すと動作した。

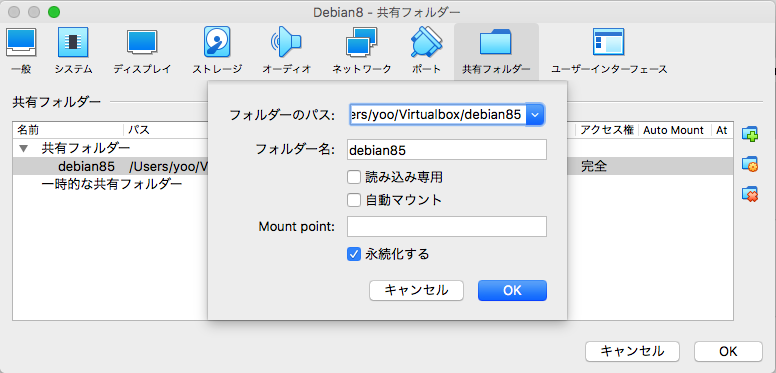
virtualbox6

あとは、マウントスクリプトをサーバに仕込めば完了

mount -t vboxsf -o uid=ユーザ,gid=ユーザ,dmode=0777,fmode=0666 共有フォルダ名 マウントパス

開発環境なのでアクセス権は甘めにしてある。

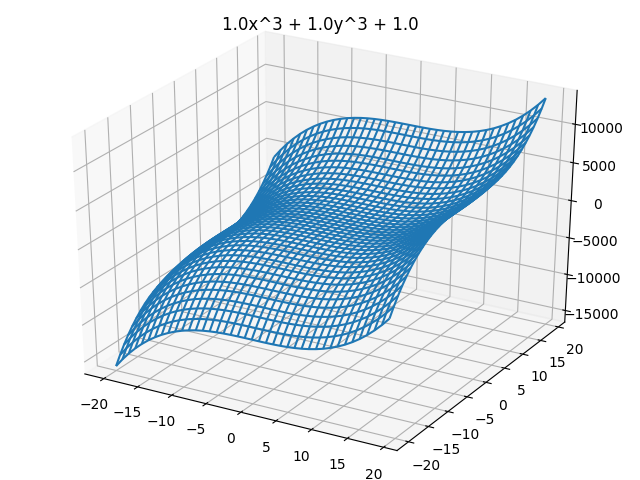
[Axes3D]曲面の3Dグラフ

Python 2018/12/04

Axes3D を利用して、曲面を3Dグラフ化する曲面の関数 $z = a x^{n} + b y^{n} + c$

描画はワイヤーフレーム plot_wireframe() を利用した。

div> Axes3D

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import sys

def calculateMesh(min_value, max_value, step):
    MESH_COUNT = 20
    x = np.arange(min_value, max_value, step)
    y = np.arange(min_value, max_value, step)
    xx, yy = np.meshgrid(np.linspace(x.min(), x.max(), MESH_COUNT), np.linspace(y.min(), y.max(), MESH_COUNT))
    return xx, yy

def plane(x, y, n, a, b, c):
    z = a*x**n + b*y**n + c
    return z

print('Graph: ax^n + bx^n + c')
step = 1
n = int(input('Please input n'))
if (n <= 0): sys.exit('invalid n!')

a, b, c = map(float, input('Please input a, b, c').split())
min_value, max_value = map(float, input('Please input min, max').split())
if (min_value >= max_value): sys.exit('invalid min, max!')

xx, yy = calculateMesh(min_value, max_value, step)
zz = plane(xx, yy, n, a, b, c)

fig = plt.figure()
ax = fig.gca(projection='3d')
ax = Axes3D(fig)
ax.plot_wireframe(xx, yy, zz)
plt.title("%sx^%s + %sy^%s + %s" % (a, n, b, n, c))
plt.show()

[Sympy]3次関数と解グラフ化(SymPy + Matplotlib編)

Python 2018/12/03

5次以上のn次方程式（非線形方程式）の一般式は困難 $x^{n} + a_{n - 1} x^{n - 1} + \dots + a_{1} x + a_{0} = 0$

scipy.optimize.fsolve, sympy.optimize.fsolve などを利用して近似的に解を求める

参考：非線形方程式の根

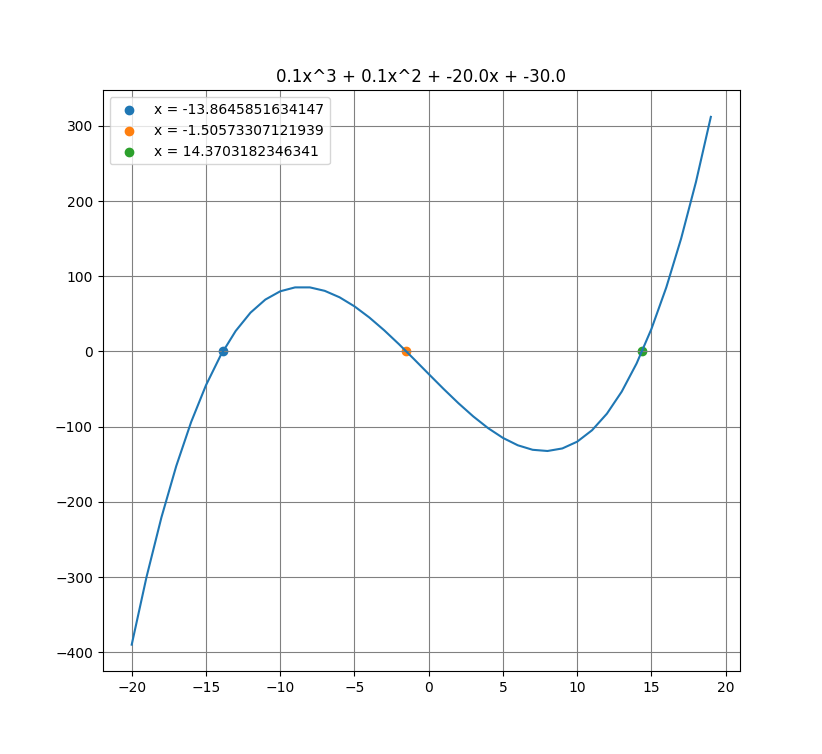
ここでは、3次関数をグラフ化してみる。

$y = a x^{3} + b x^{2} + c x + d$

*定数は任意に入力 a=0.1, b=0.1, c=-20, d=-30 x = [-20, 20]

sympy のインストール

$ pip3 install sympy

3次方程式と解

def function(a, b, c, d):
    x = Symbol('x')
    return a*x**3 + b*x**2 + c*x + d
 
def answer(a, b, c, d):
    return solve(function(a, b, c, d))

Symbol() で方程式の変数を作成し、solve() で方程式の解を計算する

実数解に虚数部が含まれる

解が実数解でも虚数部（誤差）がでるため、matplotlib の座標として扱えない。

[-10.4646576744031 + 0.e-20*I, -0.0999101526839223 + 0.e-19*I, 9.56456782708699 + 0.e-20*I]

as_coeff_Add() で配列から実数部分だけ抜き出す（解の誤差を無視） ※as_coeff_Add() は、SymPy Modules Reference参照

def convertFloat(value):
    value = (S(value).as_coeff_Add())
    if (type(value[0]) == Float):
        return value[0]

Y座標の作成

式を取得して、subs() で xに値を代入する

def plots(a, b, c, d, min_x, max_x, step):
    x = np.arange(min_x, max_x, step)
    y = [function(a, b, c, d).subs(Symbol('x'), value) for value in x]
    return x, y

サンプル

定数a, b, c, d を標準入力
グラフ用のX軸 max, min を標準入力

import matplotlib.pyplot as plt
import numpy as np
from sympy import *
import sys
 
def convertFloat(value):
    value = (S(value).as_coeff_Add())
    if (type(value[0]) == Float):
        return value[0]
        
def function(a, b, c, d):
    x = Symbol('x')
    return a*x**3 + b*x**2 + c*x + d
 
def answer(a, b, c, d):
    return solve(function(a, b, c, d))

def plots(a, b, c, d, min_x, max_x, step):
    x = np.arange(min_x, max_x, step)
    y = [function(a, b, c, d).subs(Symbol('x'), value) for value in x]
    return x, y
 
step = 0.1
a, b, c, d = map(float, input('Please input a, b, c, d.').split())
min_x, max_x = map(float, input('Please input min x, max x.').split())
 
if (min_x >= max_x): sys.exit('invalid min x max x!')

for value in answer(a, b, c, d):
    value = convertFloat(value)
    plt.scatter([value], [0], label = 'x = %s' % value)

x, y = plots(a, b, c, d, min_x, max_x, step)
plt.plot(x, y)
plt.grid(color='gray')
plt.title("%sx^3 + %sx^2 + %sx + %s" % (a, b, c, d))
plt.legend()
plt.show()

ちなみに、３次方程式で solve() の一般解は以下の通り

-(-3*c/a + b**2/a**2)/(3*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a), -(-3*c/a + b**2/a**2)/(3*(-1/2 - sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (-1/2 - sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a), -(-3*c/a + b**2/a**2)/(3*(-1/2 + sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (-1/2 + sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a)

$[- \frac{- \frac{3 c}{a} + \frac{b^{2}}{a^{2}}}{3 \sqrt[3]{\frac{\sqrt{- 4 {(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}})}^{3} + {(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}})}^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}} - \frac{\sqrt[3]{\frac{\sqrt{- 4 {(- \frac{3 c}{a} + \frac{b^{2}}{a^{2}})}^{3} + {(\frac{27 d}{a} - \frac{9 b c}{a^{2}} + \frac{2 b^{3}}{a^{3}})}^{2}}}{2} + \frac{27 d}{2 a} - \frac{9 b c}{2 a^{2}} + \frac{b^{3}}{a^{3}}}}{3} - \frac{b}{3 a},$