線形最適化問題とは？

1次式のみで定義できる式から、ある条件（制約）をもとに問題の最適解を見つけることです。
2次以上の式や、離散的な変数（連続でない）に関しての問題は対象外となります。

目的関数と制約

問題を解決するには、目的関数（求めたい解の定義式）と、問題の制約（条件）を定義します。
問題定義の関数は、 最小化と最大化の2種類あります。

例えば、生産するための最大利益、乗り換え案内などの最短経路を求めたりする問題です。

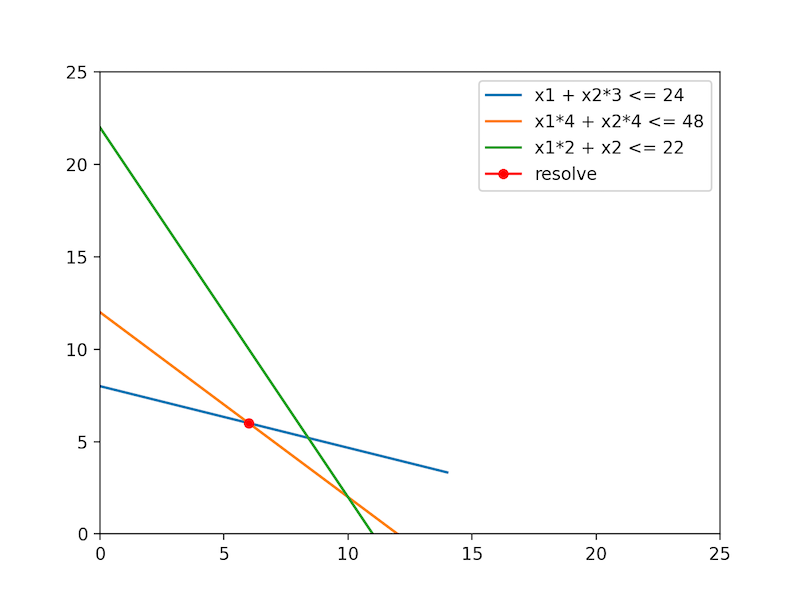
上記は3つの制約で、ある目的関数から最適解を求めたグラフ化です。
制約は（不等式）の不等号の向きで範囲が異なります。

 

PuLP とは

PuLP は COIN-OR プロジェクトで開発された線形最適化問題を解くための Pythonライブラリです。

Jupyter Notebook インストール

視覚的に確認するために、Jupyter Notebook をインストールします。
個人的には、Anaconda は入れたくないので pip3 でインストールします。

$ pip3 install jupyter

Pulp インストール

$ pip3 install pulp

Pulp の基本

決定変数

変数作成変数は、 LpVariable() で定義します。

• 連続変数（実数値）
• 0 or 1変数
• 整数値

第1引数

「インスタンス名」で必須です。

第2引数

• lowBound：変数の下限値（デフォルト：None）
• upBound：変数の上限値（デフォルト：None）
• cat：変数の種類（デフォルト：連続変数 = pulp.LpContinuous）

変数の利用例

x1 = pulp.LpVariable('x1', 0)
x2 = pulp.LpVariable('x2', 0) 

問題定義のモデル作成

目的関数と制約

目的関数を LpProblem() でインスタンスを作成し、制約を追加してきます。

最大化モデル作成

LpProblem(sense= LpMaximize)

最小化モデル作成

LpProblem(sense=LpMinimize)

ラベル付きの例

problem = pulp.LpProblem('最大化問題', sense=pulp. LpMaximize)

作成したインスタンスに、目的関数、制約の式を追加します。

problem = pulp.LpProblem('生産計画問題', sense=pulp. LpMaximize)
problem+= x1 + 2*x2, '目的関数 利益見込み'
problem+= x1 + 3*x2 <= 24, '原料制約'
problem+= 4*x1 + 4*x2 <= 48, '労働時間制約'
problem+= 2*x1 + x2 <= 22, '機会稼働制約'
problem

最適解の計算

定義した問題定義を実際に解くには、 solve() を利用しますが、戻り値は実際の解ではなく、成功フラグになります。

result = problem.solve()

実行結果のステータス

実行結果のステータスを確認するのに、 LpStatus() を利用します。

print(pulp.LpStatus[result])

ステータスの種類

{
 -3: 'Undefined',
 -2: 'Unbounded',
 -1: 'Infeasible',
 0: 'Not Solved',
 1: 'Optimal'
}

目的関数の最適値（最大・最小値）

目的関数の最適解は、 value(モデル.objective) で取得します。

print(pulp.value(problem.objective))

最適解を求める

解の取得

最適解を求めたら、解を取得します。
定義した決定変数を variables() 、それぞれの解を value(オブジェクト) で取得します。

for v in problem.variables():
    print(f’{v} = {pulp.value(v)}’)

結果

$ python3 2-1.py 
x1 = 6.0
x2 = 6.0

Jupiter Notebook