5次以上のn次方程式（非線形方程式）の一般式は困難 $$x^n+a_{n-1}{x}^{n-<!--\; -\; -->1}+\cdots <!--\; \cdots \; -->+a_{1}x+a_0=0$$

scipy.optimize.fsolve, sympy.optimize.fsolve などを利用して近似的に解を求める

参考：非線形方程式の根

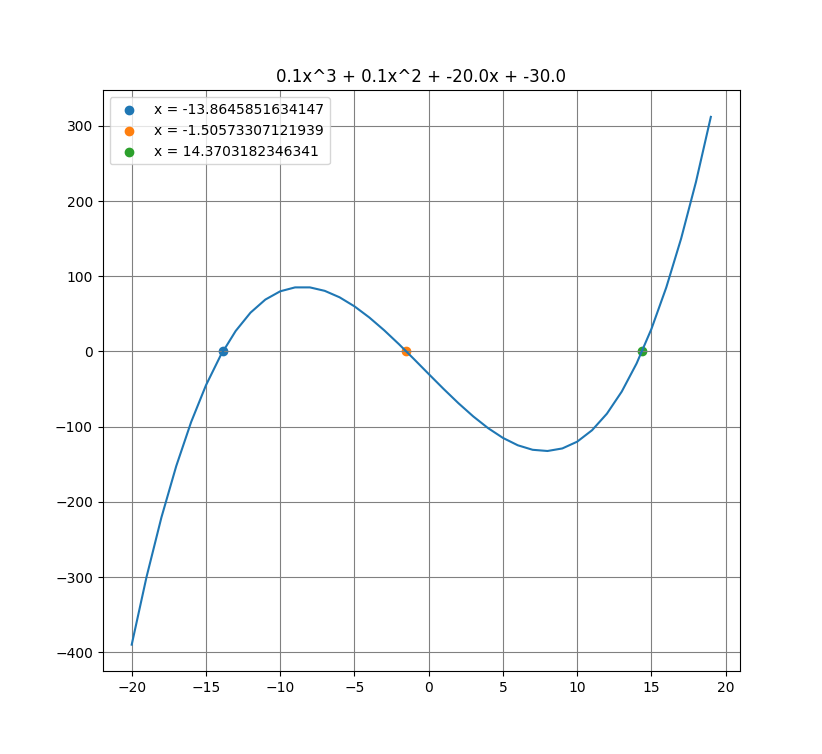
ここでは、3次関数をグラフ化してみる。

*定数は任意に入力 a=0.1, b=0.1, c=-20, d=-30 x = [-20, 20]

sympy のインストール

$ pip3 install sympy

3次方程式と解

def function(a, b, c, d):
    x = Symbol('x')
    return a*x**3 + b*x**2 + c*x + d
 
def answer(a, b, c, d):
    return solve(function(a, b, c, d))

Symbol() で方程式の変数を作成し、solve() で方程式の解を計算する

実数解に虚数部が含まれる

解が実数解でも虚数部（誤差）がでるため、matplotlib の座標として扱えない。

[-10.4646576744031 + 0.e-20*I, -0.0999101526839223 + 0.e-19*I, 9.56456782708699 + 0.e-20*I]

as_coeff_Add() で配列から実数部分だけ抜き出す（解の誤差を無視） ※as_coeff_Add() は、SymPy Modules Reference参照

def convertFloat(value):
    value = (S(value).as_coeff_Add())
    if (type(value[0]) == Float):
        return value[0]

Y座標の作成

式を取得して、subs() で xに値を代入する

def plots(a, b, c, d, min_x, max_x, step):
    x = np.arange(min_x, max_x, step)
    y = [function(a, b, c, d).subs(Symbol('x'), value) for value in x]
    return x, y

サンプル

• 定数a, b, c, d を標準入力
• グラフ用のX軸 max, min を標準入力

import matplotlib.pyplot as plt
import numpy as np
from sympy import *
import sys
 
def convertFloat(value):
    value = (S(value).as_coeff_Add())
    if (type(value[0]) == Float):
        return value[0]
        
def function(a, b, c, d):
    x = Symbol('x')
    return a*x**3 + b*x**2 + c*x + d
 
def answer(a, b, c, d):
    return solve(function(a, b, c, d))

def plots(a, b, c, d, min_x, max_x, step):
    x = np.arange(min_x, max_x, step)
    y = [function(a, b, c, d).subs(Symbol('x'), value) for value in x]
    return x, y
 
step = 0.1
a, b, c, d = map(float, input('Please input a, b, c, d.').split())
min_x, max_x = map(float, input('Please input min x, max x.').split())
 
if (min_x >= max_x): sys.exit('invalid min x max x!')

for value in answer(a, b, c, d):
    value = convertFloat(value)
    plt.scatter([value], [0], label = 'x = %s' % value)

x, y = plots(a, b, c, d, min_x, max_x, step)
plt.plot(x, y)
plt.grid(color='gray')
plt.title("%sx^3 + %sx^2 + %sx + %s" % (a, b, c, d))
plt.legend()
plt.show()

ちなみに、３次方程式で solve() の一般解は以下の通り

-(-3*c/a + b**2/a**2)/(3*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a), -(-3*c/a + b**2/a**2)/(3*(-1/2 - sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (-1/2 - sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a), -(-3*c/a + b**2/a**2)/(3*(-1/2 + sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (-1/2 + sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a)

$$[-<!--\; -\; -->\frac{-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2}}{3\sqrt[3]{\frac{\sqrt{-<!--\; -\; -->4{(-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2})}^3+{(\frac{27d}{a}-<!--\; -\; -->\frac{9bc}{a^2}+\frac{2b^3}{a^3})}^2}}{2}+\frac{27d}{2a}-<!--\; -\; -->\frac{9bc}{2a^2}+\frac{b^3}{a^3}}}-<!--\; -\; -->\frac{\sqrt[3]{\frac{\sqrt{-<!--\; -\; -->4{(-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2})}^3+{(\frac{27d}{a}-<!--\; -\; -->\frac{9bc}{a^2}+\frac{2b^3}{a^3})}^2}}{2}+\frac{27d}{2a}-<!--\; -\; -->\frac{9bc}{2a^2}+\frac{b^3}{a^3}}}{3}-<!--\; -\; -->\frac{b}{3a},-<!--\; -\; -->\frac{-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2}}{3(-<!--\; -\; -->\frac{1}{2}-<!--\; -\; -->\frac{\sqrt{3}i}{2})\sqrt[3]{\frac{\sqrt{-<!--\; -\; -->4{(-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2})}^3+{(\frac{27d}{a}-<!--\; -\; -->\frac{9bc}{a^2}+\frac{2b^3}{a^3})}^2}}{2}+\frac{27d}{2a}-<!--\; -\; -->\frac{9bc}{2a^2}+\frac{b^3}{a^3}}}-<!--\; -\; -->\frac{(-<!--\; -\; -->\frac{1}{2}-<!--\; -\; -->\frac{\sqrt{3}i}{2})\sqrt[3]{\frac{\sqrt{-<!--\; -\; -->4{(-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2})}^3+{(\frac{27d}{a}-<!--\; -\; -->\frac{9bc}{a^2}+\frac{2b^3}{a^3})}^2}}{2}+\frac{27d}{2a}-<!--\; -\; -->\frac{9bc}{2a^2}+\frac{b^3}{a^3}}}{3}-<!--\; -\; -->\frac{b}{3a},-<!--\; -\; -->\frac{-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2}}{3(-<!--\; -\; -->\frac{1}{2}+\frac{\sqrt{3}i}{2})\sqrt[3]{\frac{\sqrt{-<!--\; -\; -->4{(-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2})}^3+{(\frac{27d}{a}-<!--\; -\; -->\frac{9bc}{a^2}+\frac{2b^3}{a^3})}^2}}{2}+\frac{27d}{2a}-<!--\; -\; -->\frac{9bc}{2a^2}+\frac{b^3}{a^3}}}-<!--\; -\; -->\frac{(-<!--\; -\; -->\frac{1}{2}+\frac{\sqrt{3}i}{2})\sqrt[3]{\frac{\sqrt{-<!--\; -\; -->4{(-<!--\; -\; -->\frac{3c}{a}+\frac{b^2}{a^2})}^3+{(\frac{27d}{a}-<!--\; -\; -->\frac{9bc}{a^2}+\frac{2b^3}{a^3})}^2}}{2}+\frac{27d}{2a}-<!--\; -\; -->\frac{9bc}{2a^2}+\frac{b^3}{a^3}}}{3}-<!--\; -\; -->\frac{b}{3a}]$$