Matplotlib で3直線で囲まれた範囲を塗りつぶしをしてみます。
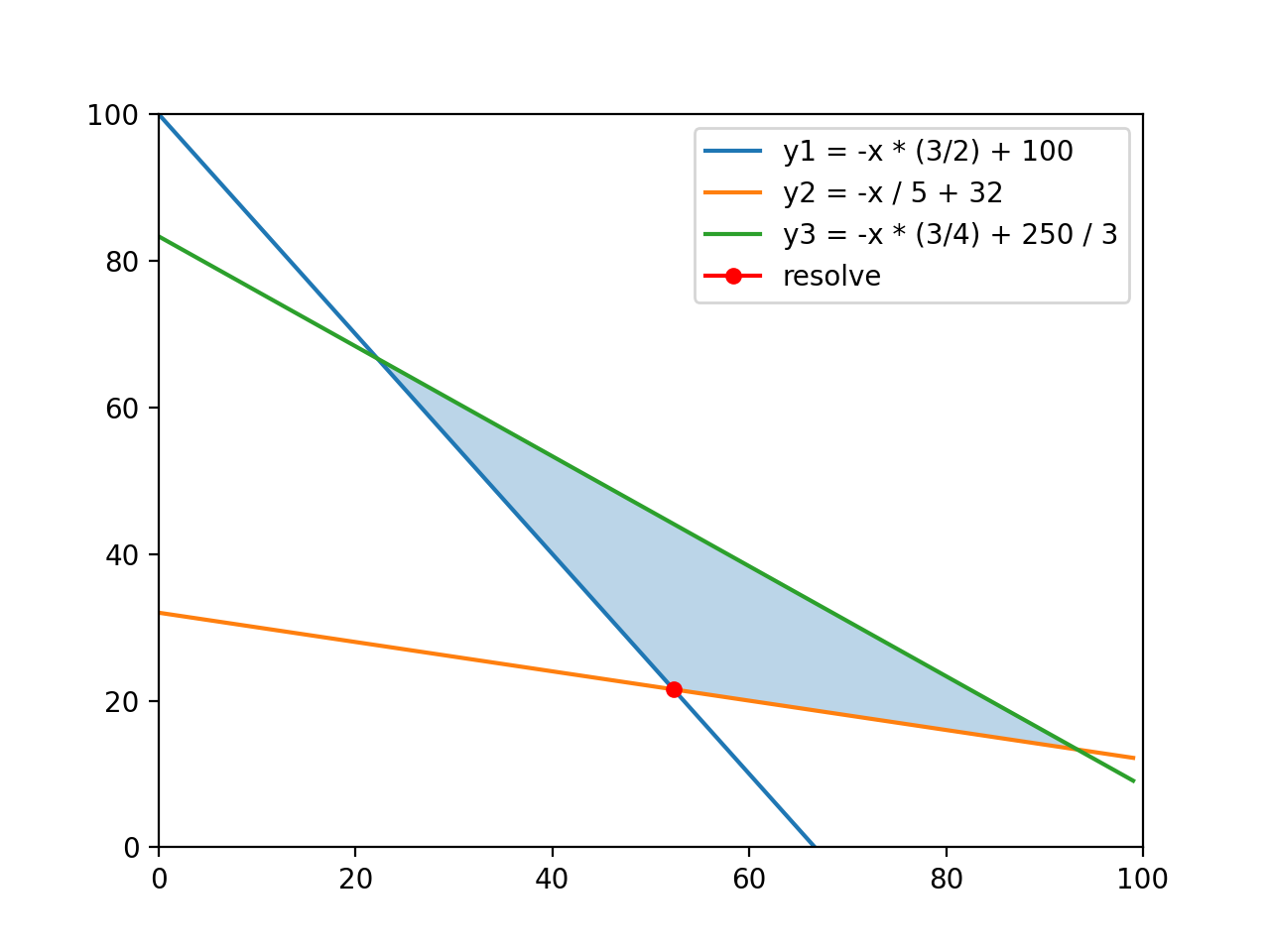
3直線の定義
まず、x の範囲を適当に設定し、3直線を定義します。
x = np.arange(0, 100, 0.1)
y1 = -x * (3/2) + 100
y2 = -x / 5 + 32
y3 = -x * (3/4) + 250 / 3
プロット
plt.plot(x, y1, label="y1: 3*x1 + 2*x2 >= 200")
plt.plot(x, y2, label="y2: x1 + 5*x2 >= 160")
plt.plot(x, y3, label="y3: 4*x1 + 3*x2 >= 250")
塗りつぶし
実際の塗りつぶしは、fill_between() 機能を利用します。
ですが、fill_between() は3式以上には対応していないため、2つのデータに落とし込む必要があります。
2式(データ)に落とし込む
numpy の maximum(), minimum() で2式の最大値または最小値を取得します。
まず y1 y2 のグラフのような条件下でデータ y4 を設定します。
y4 = np.maximum(y1, y2)
グラフを塗りつぶす
今度は y3, y4 を fill_between() と where パラメータで塗りつぶします。
グラフでもわかるように y4(y1, y2 条件のデータ) <= y3 となります。
ax = plt.axes()
ax.fill_between(
x,
y3,
y4,
where=y3 > y4,
alpha=0.3,
interpolate=True,
)
第1引数は、x軸の値、第2,3引数は2式のデータ、オプションとして where など設定します
もし、3式の交点がわあかっていれば、fill() を使って交点指定で塗りつぶしても良いかと思います。
線形最適化問題とは?
1次式のみで定義できる式から、ある条件(制約)をもとに問題の最適解を見つけることです。
2次以上の式や、離散的な変数(連続でない)に関しての問題は対象外となります。
目的関数と制約
問題を解決するには、目的関数(求めたい解の定義式)と、問題の制約(条件)を定義します。
問題定義の関数は、 最小化と最大化の2種類あります。
例えば、生産するための最大利益、乗り換え案内などの最短経路を求めたりする問題です。
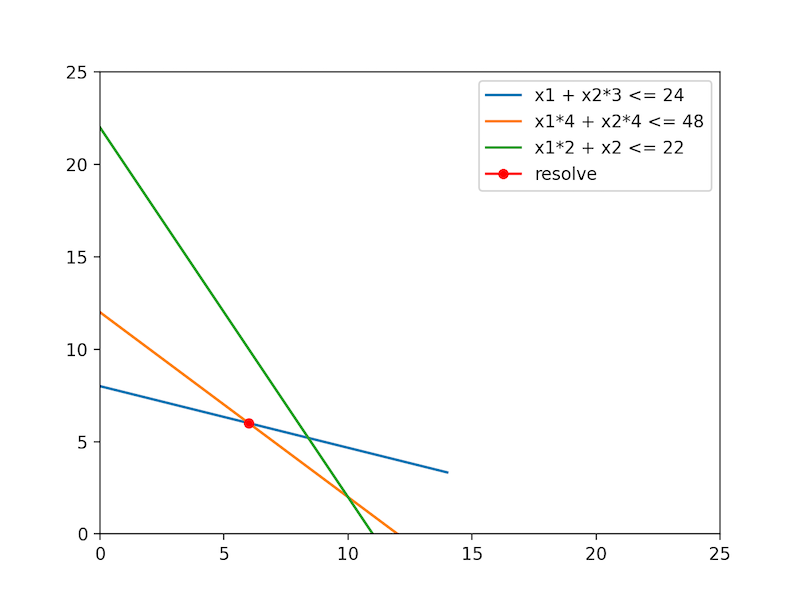
上記は3つの制約で、ある目的関数から最適解を求めたグラフ化です。
制約は(不等式)の不等号の向きで範囲が異なります。
PuLP とは
PuLP は COIN-OR プロジェクトで開発された線形最適化問題を解くための Pythonライブラリです。
Jupyter Notebook インストール
視覚的に確認するために、Jupyter Notebook をインストールします。
個人的には、Anaconda は入れたくないので pip3 でインストールします。
$ pip3 install jupyter
Pulp インストール
$ pip3 install pulp
Pulp の基本
決定変数
変数作成変数は、 LpVariable() で定義します。
- 連続変数(実数値)
- 0 or 1変数
- 整数値
第1引数
「インスタンス名」で必須です。
第2引数
- lowBound:変数の下限値(デフォルト:None)
- upBound:変数の上限値(デフォルト:None)
- cat:変数の種類(デフォルト:連続変数 = pulp.LpContinuous)
変数の利用例
x1 = pulp.LpVariable('x1', 0)
x2 = pulp.LpVariable('x2', 0)
問題定義のモデル作成
目的関数と制約
目的関数を LpProblem() でインスタンスを作成し、制約を追加してきます。
最大化モデル作成
LpProblem(sense= LpMaximize)
最小化モデル作成
LpProblem(sense=LpMinimize)
ラベル付きの例
problem = pulp.LpProblem('最大化問題', sense=pulp. LpMaximize)
作成したインスタンスに、目的関数、制約の式を追加します。
problem = pulp.LpProblem('生産計画問題', sense=pulp. LpMaximize)
problem+= x1 + 2*x2, '目的関数 利益見込み'
problem+= x1 + 3*x2 <= 24, '原料制約'
problem+= 4*x1 + 4*x2 <= 48, '労働時間制約'
problem+= 2*x1 + x2 <= 22, '機会稼働制約'
problem
最適解の計算
定義した問題定義を実際に解くには、 solve() を利用しますが、戻り値は実際の解ではなく、成功フラグになります。
result = problem.solve()
実行結果のステータス
実行結果のステータスを確認するのに、 LpStatus() を利用します。
print(pulp.LpStatus[result])
ステータスの種類
{
-3: 'Undefined',
-2: 'Unbounded',
-1: 'Infeasible',
0: 'Not Solved',
1: 'Optimal'
}
目的関数の最適値(最大・最小値)
目的関数の最適解は、 value(モデル.objective) で取得します。
print(pulp.value(problem.objective))
最適解を求める
解の取得
最適解を求めたら、解を取得します。
定義した決定変数を variables() 、それぞれの解を value(オブジェクト) で取得します。
for v in problem.variables():
print(f’{v} = {pulp.value(v)}’)
結果
$ python3 2-1.py
x1 = 6.0
x2 = 6.0
Jupiter Notebook

Python単体 と Anaconda は比較的衝突しやすいので、Anacondaを削除してみる
anaconda-clean のインストールと実行
$ conda install anaconda-clean
$ anaconda-clean
anaconda_backup の削除
$ rm -rf ~/.anaconda_backup
<
h2 class="h2">anaconda 本体の削除 環境によってパスが異なるが、which anaconda などでパスを確認して削除
$ cd ~/.pyenv
$ rm -rf versions
$ cd .pyenv/shims
$ rm -rf anaconda*
<
h2 class="h2">.bash_profile から環境変数の削除 ~/.bash_profile に環境変数が追加されていた場合はこれを削除
ターミナルを再起動すると anaconda は動作しない
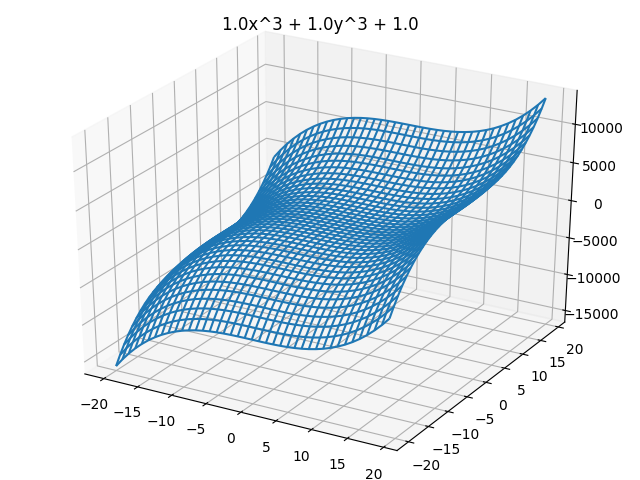
Axes3D を利用して、曲面を3Dグラフ化する 曲面の関数
描画はワイヤーフレーム plot_wireframe() を利用した。
<
div>
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import sys
def calculateMesh(min_value, max_value, step):
MESH_COUNT = 20
x = np.arange(min_value, max_value, step)
y = np.arange(min_value, max_value, step)
xx, yy = np.meshgrid(np.linspace(x.min(), x.max(), MESH_COUNT), np.linspace(y.min(), y.max(), MESH_COUNT))
return xx, yy
def plane(x, y, n, a, b, c):
z = a*x**n + b*y**n + c
return z
print('Graph: ax^n + bx^n + c')
step = 1
n = int(input('Please input n'))
if (n <= 0): sys.exit('invalid n!')
a, b, c = map(float, input('Please input a, b, c').split())
min_value, max_value = map(float, input('Please input min, max').split())
if (min_value >= max_value): sys.exit('invalid min, max!')
xx, yy = calculateMesh(min_value, max_value, step)
zz = plane(xx, yy, n, a, b, c)
fig = plt.figure()
ax = fig.gca(projection='3d')
ax = Axes3D(fig)
ax.plot_wireframe(xx, yy, zz)
plt.title("%sx^%s + %sy^%s + %s" % (a, n, b, n, c))
plt.show()
5次以上のn次方程式(非線形方程式)の一般式は困難
scipy.optimize.fsolve, sympy.optimize.fsolve などを利用して近似的に解を求める
参考:非線形方程式の根
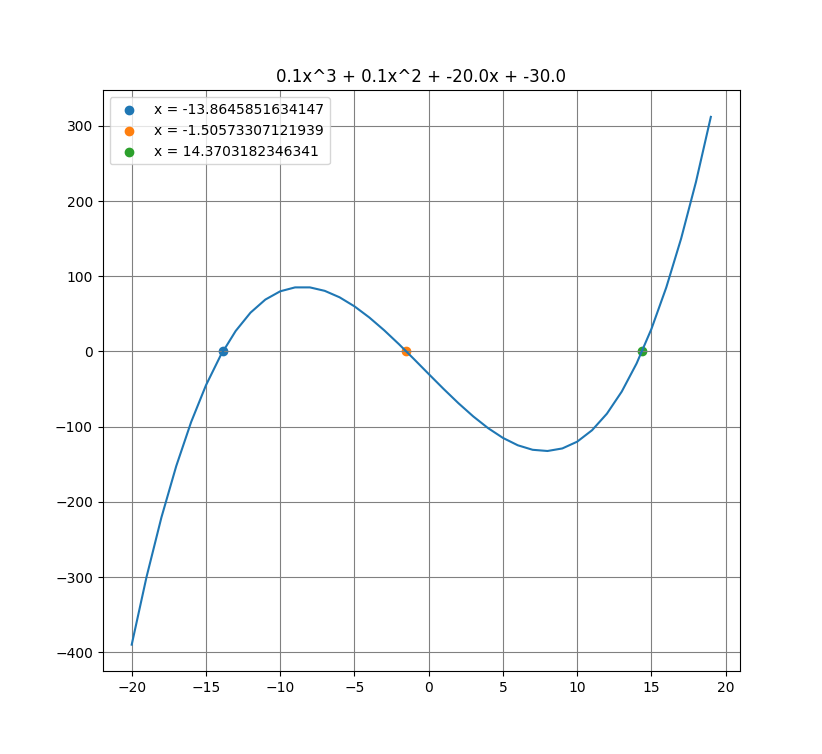
ここでは、3次関数をグラフ化してみる。
*定数は任意に入力
a=0.1, b=0.1, c=-20, d=-30
x = [-20, 20]
sympy のインストール
$ pip3 install sympy3次方程式と解
def function(a, b, c, d):
x = Symbol('x')
return a*x**3 + b*x**2 + c*x + d
def answer(a, b, c, d):
return solve(function(a, b, c, d))
Symbol() で方程式の変数を作成し、solve() で方程式の解を計算する
実数解に虚数部が含まれる
解が実数解でも虚数部(誤差)がでるため、matplotlib の座標として扱えない。
[-10.4646576744031 + 0.e-20*I, -0.0999101526839223 + 0.e-19*I, 9.56456782708699 + 0.e-20*I]
as_coeff_Add() で配列から実数部分だけ抜き出す(解の誤差を無視) ※as_coeff_Add() は、SymPy Modules Reference参照
def convertFloat(value):
value = (S(value).as_coeff_Add())
if (type(value[0]) == Float):
return value[0]
Y座標の作成
式を取得して、subs() で xに値を代入する
def plots(a, b, c, d, min_x, max_x, step):
x = np.arange(min_x, max_x, step)
y = [function(a, b, c, d).subs(Symbol('x'), value) for value in x]
return x, y
サンプル
- 定数a, b, c, d を標準入力
- グラフ用のX軸 max, min を標準入力
import matplotlib.pyplot as plt
import numpy as np
from sympy import *
import sys
def convertFloat(value):
value = (S(value).as_coeff_Add())
if (type(value[0]) == Float):
return value[0]
def function(a, b, c, d):
x = Symbol('x')
return a*x**3 + b*x**2 + c*x + d
def answer(a, b, c, d):
return solve(function(a, b, c, d))
def plots(a, b, c, d, min_x, max_x, step):
x = np.arange(min_x, max_x, step)
y = [function(a, b, c, d).subs(Symbol('x'), value) for value in x]
return x, y
step = 0.1
a, b, c, d = map(float, input('Please input a, b, c, d.').split())
min_x, max_x = map(float, input('Please input min x, max x.').split())
if (min_x >= max_x): sys.exit('invalid min x max x!')
for value in answer(a, b, c, d):
value = convertFloat(value)
plt.scatter([value], [0], label = 'x = %s' % value)
x, y = plots(a, b, c, d, min_x, max_x, step)
plt.plot(x, y)
plt.grid(color='gray')
plt.title("%sx^3 + %sx^2 + %sx + %s" % (a, b, c, d))
plt.legend()
plt.show()
ちなみに、3次方程式で solve() の一般解は以下の通り
-(-3*c/a + b**2/a**2)/(3*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a), -(-3*c/a + b**2/a**2)/(3*(-1/2 - sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (-1/2 - sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a), -(-3*c/a + b**2/a**2)/(3*(-1/2 + sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)) - (-1/2 + sqrt(3)*I/2)*(sqrt(-4*(-3*c/a + b**2/a**2)**3 + (27*d/a - 9*b*c/a**2 + 2*b**3/a**3)**2)/2 + 27*d/(2*a) - 9*b*c/(2*a**2) + b**3/a**3)**(1/3)/3 - b/(3*a)
matplotlib の plot() はデータをプロットするが、Sympy の plot() を利用すると一般式をグラフ化できる。 数式を手っ取り早く視覚化するには使える
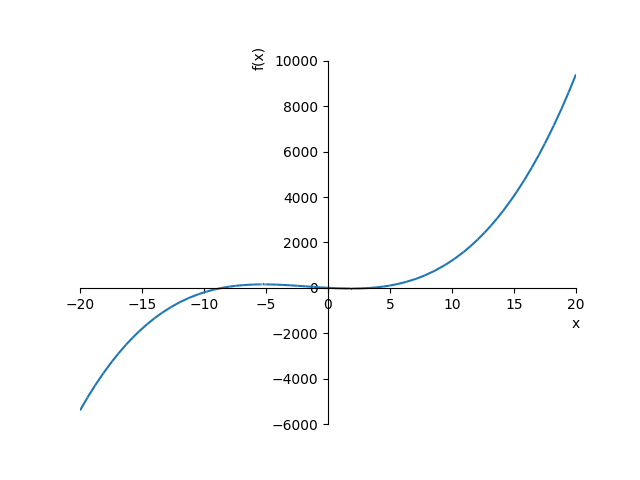 Sympy の plot() の第1引数に数式、第2引数にX軸の情報を入れる
Sympy の plot() の第1引数に数式、第2引数にX軸の情報を入れる
サンプル
from sympy.plotting import plot
from sympy import Number, NumberSymbol, Symbol, Eq, solve
import sys
def function():
x = Symbol('x')
return a*x**3 + b*x**2 + c*x + d
a, b, c, d = map(float, input('Please input a, b, c, d.').split())
min_x, max_x = map(float, input('Please input min x, max x.').split())
if (min_x >= max_x): sys.exit('invalid min x max x!')
x = Symbol('x')
y = function()
min_y = y.subs([(x, min_x)])
max_y = y.subs([(x, max_x)])
plot(y, (x, min_x, max_x))
ちなみに、以下でxの最大最小から、yの最大最小を求めている。
min_y = y.subs([(x, min_x)])
max_y = y.subs([(x, max_x)])
2次関数の解はSympy.solve, scipy.optimize.fsolve を使っても求められるが、ここでは非効率だが2次関数の一般式を作成、解を求めてグラフ化してみる。
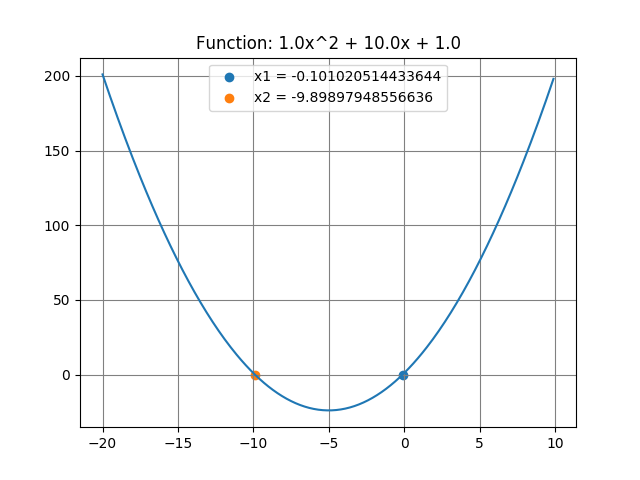
2次関数の定数を標準入力
a, b, c = map(float, input('Please input a, b, c ').split())
*Python3 の記述
解の公式
def answer(a, b, c):
x1 = (-b + np.sqrt((b ** 2) - (4 * a * c))) / (2 * a)
x2 = (-b - np.sqrt((b ** 2) - (4 * a * c))) / (2 * a)
return [x1, x2]
判別式
解がない(虚数)だと、プロットできないので判別式の関数を作成
((b**2) - (4 * a * c)) >= 0
X座標の配列
最大値、最小値、X軸プロット間隔を設定
def plotX(a, b, c):
max_x = 10
min_x = -10
x = np.arange(min_x, max_x, 0.1)
return x
*最終的に最大値、最小値は、解によって動的に変化させる
Y座標の配列
二次方程式を記述
def plotY(a, b, c):
return a*x**2 + b*x + c
サンプル
import matplotlib.pyplot as plt
import numpy as np
from sympy import *
def hasAnswer(a, b, c):
return ((b * b) - (4 * a * c)) >= 0
def answer(a, b, c):
x1 = (-b + sqrt((b ** 2) - (4 * a * c))) / (2 * a)
x2 = (-b - sqrt((b ** 2) - (4 * a * c))) / (2 * a)
return [x1, x2]
def plotX(a, b, c):
max_x = 10
min_x = -10
if (hasAnswer(a, b, c)):
x = answer(a, b, c)
x1 = x[0]
x2 = x[1]
center = (x2 - x1) * 0.5
band = abs(x2 - x1)
if band <= 1:
band = 10
max_x = round(x1 + band, 0)
min_x = round(x2 - band, 0)
x = np.arange(min_x, max_x, 0.1)
return x
def plotY(a, b, c):
return a*x**2 + b*x + c
def plotScatterX(plt, a, b, c):
if (hasAnswer(a, b, c)):
x = answer(a, b, c)
plt.scatter([x[0]], [0], label = 'x1 = %s' % x[0])
plt.scatter([x[1]], [0], label = 'x2 = %s' % x[1])
return
print('Simulatenous Equations. a * x^2 + b * x + c')
a, b, c = map(float, input('Please input a, b, c').split())
x = plotX(a, b, c)
y = plotY(a, b, c)
plt.plot(x, y)
plotScatterX(plt, a, b, c)
plt.title('Function: %sx^2 + %sx + %s' % (a, b, c))
plt.grid(color='gray')
plt.legend()
plt.show()
Debian の最新バージョンは python3 が Universe Repository に含まれている。
# aptitude update
# aptitude install python3
pip インストール
# aptitude install python3-pippyenv インストール
$ git clone git://github.com/yyuu/pyenv.git ~/.pyenv
$ git clone https://github.com/yyuu/pyenv-pip-rehash.git ~/.pyenv/plugins/pyenv-pip-rehash
.bashrc に環境変数追加
$ echo 'export PYENV_ROOT="$HOME/.pyenv"' >> ~/.bashrc
$ echo 'export PATH="$PYENV_ROOT/bin:$PATH"' >> ~/.bashrc
$ echo 'eval "$(pyenv init -)"' >> ~/.bashrc
$ source ~/.bashrc
pyenv 動作確認
$ pyenv
...
Some useful pyenv commands are:
commands List all available pyenv commands
local Set or show the local application-specific Python version
global Set or show the global Python version
shell Set or show the shell-specific Python version
install Install a Python version using python-build
uninstall Uninstall a specific Python version
rehash Rehash pyenv shims (run this after installing executables)
version Show the current Python version and its origin
versions List all Python versions available to pyenv
which Display the full path to an executable
whence List all Python versions that contain the given executable
...
Anaconda インストール
$ pyenv install anaconda3-5.1.0
Downloading Anaconda3-5.1.0-Linux-x86_64.sh...
-> https://repo.continuum.io/archive/Anaconda3-5.1.0-Linux-x86_64.sh
Installing Anaconda3-5.1.0-Linux-x86_64...
Installed Anaconda3-5.1.0-Linux-x86_64 to /home/yoo/.pyenv/versions/anaconda3-5.1.0
*デフォルト /tmp にインストールされるようなので容量には注意 ソースインストールの場合 Download Anaconda Distribution からダウンロードしてインストール
$ wget https://repo.continuum.io/archive/Anaconda3-5.1.0-Linux-x86_64.sh
For full documentation, see: https://github.com/pyenv/pyenv#readme
$sh Anaconda3-5.1.0-Linux-x86_64.sh
Anaconda 設定/アップデート
$ pyenv global anaconda3-5.1.0
$ pyenv versions
system
* anaconda3-5.1.0 (set by /home/yoo/.pyenv/version)
$ conda update conda
Solving environment: done
....
The following packages will be downloaded:
package | build
---------------------------|-----------------
conda-4.5.0 | py36_0 1.0 MB
The following packages will be UPDATED:
conda: 4.4.10-py36_0 --> 4.5.0-py36_0
Proceed ([y]/n)?
....
Preparing transaction: done
Verifying transaction: done
Executing transaction: done
これで、python コマンドでも python3が利用できる。
$ python --version
Python 3.6.4 :: Anaconda, Inc.
Anaconda でライブラリインストール
pip でなく Anaconda でライブラリをインストールする
$ conda install matplotlibpsycopg2 を利用して PostgreSQL に接続する
import numpy as np
import psycopg2 as pg
import psycopg2.extras
connection = pg.connect("host=localhost port=5432 dbname=db_name user=postgres")
cursor = connection.cursor(cursor_factory=psycopg2.extras.DictCursor)
cursor.execute("SELECT * FROM users")
results = cursor.fetchall()
values = []
for row in results:
values.append(dict(row))
print(values)
cursor.close()
connection.close()
- PostgreSQL接続は、psycopg2.connect("DB設定")
- connection.cursor() で cursor 作成
- ディクショナリ形式で取得するには、psycopg2.exras.DictCuror を引数にする
- cursor.execute() でSQLを実行
- cursor.fetchall() でデータ取得
- dict() でディクショナリ形式にし、append() で連想配列にする
Chainerインストール
$ pip install --upgrade pip
$ pip install chainerchainer/chainerからサンプルをダウンロード
$ brew tap caskroom/cask
サンプルを動かす
機械学習のHello-World「train_mnist.py 」を動かしてみる。 *初回時は画像素材をダウンロード *デフォルト設定だと20回学習
$ python3 train_mnist.py
GPU: -1
# unit: 1000
# Minibatch-size: 100
# epoch: 20
Downloading from http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz...
Downloading from http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz...
Downloading from http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz...
Downloading from http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz...
epoch main/loss validation/main/loss main/accuracy validation/main/accuracy elapsed_time
1 0.191203 0.107441 0.942 0.9668 20.6231
2 0.0746089 0.0724309 0.9769 0.9779 43.3326
3 0.0483745 0.0715516 0.9848 0.9798 66.719
4 0.0341754 0.0789327 0.988833 0.9795 89.0281
5 0.0292061 0.0925641 0.9908 0.9752 109.421
6 0.0256707 0.0715148 0.991683 0.9806 132.37
7 0.0188833 0.0750383 0.993767 0.9808 153.467
8 0.0178651 0.0916148 0.993967 0.9798 173.683
9 0.0190301 0.0876899 0.9941 0.9805 194.203
10 0.0147034 0.0869119 0.995183 0.9813 217.873
11 0.0140121 0.088435 0.995817 0.9802 242.648
12 0.0151053 0.0939939 0.99495 0.9823 268.818
13 0.0103742 0.0957632 0.996717 0.9829 292.792
14 0.00854318 0.0905123 0.997467 0.9821 317.834
15 0.00866289 0.118263 0.99745 0.9766 343.89
16 0.0151463 0.0986677 0.99545 0.9817 368.499
17 0.00866498 0.0853589 0.99735 0.9842 395.06
18 0.00716674 0.131718 0.997883 0.9776 421.821
19 0.00858464 0.111747 0.997567 0.9834 448.749
20 0.0127154 0.103087 0.996683 0.9814 474.769
OpenCV3インストール
運よくNVIDIA製のグラボを積んだマシンを持っていたらGPUモードで計算させられます。 (自分は持ってない・・・) NVIDIAからCUDAダウンロード
$ brew tap homebrew/science
$ brew install opencv3 --with-contrib --with-python3 --without-python
$ vi .bashrc
export PATH=/Developer/NVIDIA/CUDA-8.0/bin:$PATH
export DYLD_LIBRARY_PATH=/Developer/NVIDIA/CUDA-7.5/lib:$DYLD_LIBRARY_PATH
if [ -f ~/.bashrc ]; then
. ~/.bashrc
fi
OpenCV3ライブラリリンク
$ ln -s /usr/local/Cellar/opencv3/3.2.0/lib/python3.6/site-packages/cv2.cpython-36m-darwin.so ~/.pyenv/versions/3.6.1/lib/python3.6/site-packages/
$ ln -s /usr/local/Cellar/opencv3/3.2.0/lib/python3.6/site-packages/cv2.cpython-36m-darwin.so ~/.pyenv/versions/anaconda3-4.4.0/lib/python3.6/site-packages/
OpenCV読み込みテスト
$ python
>>import cv2
>>
