2次関数の解はSympy.solve, scipy.optimize.fsolve を使っても求められるが、ここでは非効率だが2次関数の一般式を作成、解を求めてグラフ化してみる。

2次関数の定数を標準入力

a, b, c = map(float, input('Please input a, b, c ').split())

*Python3 の記述

解の公式

$$y =\hspace{0.17em}a{x}^2+bx + c$$ $$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

def answer(a, b, c):
    x1 = (-b + np.sqrt((b ** 2) - (4 * a * c))) / (2 * a)
    x2 = (-b - np.sqrt((b ** 2) - (4 * a * c))) / (2 * a)
    return [x1, x2]

判別式

解がない（虚数）だと、プロットできないので判別式の関数を作成

((b**2) - (4 * a * c)) >= 0

X座標の配列

最大値、最小値、X軸プロット間隔を設定

def plotX(a, b, c):
    max_x = 10
    min_x = -10
    x = np.arange(min_x, max_x, 0.1)
    return x

*最終的に最大値、最小値は、解によって動的に変化させる

Y座標の配列

二次方程式を記述

def plotY(a, b, c):
    return a*x**2 + b*x + c

サンプル

import matplotlib.pyplot as plt
import numpy as np
from sympy import *

def hasAnswer(a, b, c):
    return ((b * b) - (4 * a * c)) >= 0

def answer(a, b, c):
    x1 = (-b + sqrt((b ** 2) - (4 * a * c))) / (2 * a)
    x2 = (-b - sqrt((b ** 2) - (4 * a * c))) / (2 * a)
    return [x1, x2]

def plotX(a, b, c):
    max_x = 10
    min_x = -10

    if (hasAnswer(a, b, c)):
        x = answer(a, b, c)
        x1 = x[0]
        x2 = x[1]
        center = (x2 - x1) * 0.5

        band = abs(x2 - x1)
        if band <= 1:
            band = 10

        max_x = round(x1 + band, 0)
        min_x = round(x2 - band, 0)

    x = np.arange(min_x, max_x, 0.1)
    return x

def plotY(a, b, c):
    return a*x**2 + b*x + c

def plotScatterX(plt, a, b, c):
    if (hasAnswer(a, b, c)):
        x = answer(a, b, c)
        plt.scatter([x[0]], [0], label = 'x1 = %s' % x[0])
        plt.scatter([x[1]], [0], label = 'x2 = %s' % x[1])
    return

print('Simulatenous Equations. a * x^2 + b * x + c')
a, b, c = map(float, input('Please input a, b, c').split())

x = plotX(a, b, c)
y = plotY(a, b, c)
plt.plot(x, y)

plotScatterX(plt, a, b, c)

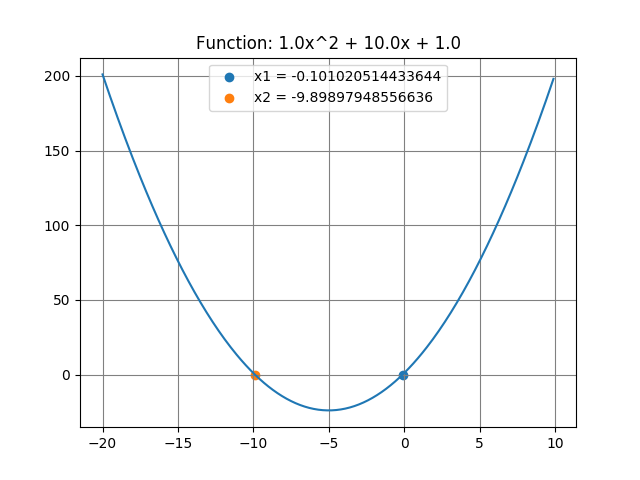
plt.title('Function: %sx^2 + %sx + %s' % (a, b, c))

plt.grid(color='gray')
plt.legend()
plt.show()