Apache2.4 を起動したところ以下のエラー
client denied by server configuration
/etc/apache2/apache2.conf の設定をみると
Options FollowSymLinks
AllowOverride None
Require all denied
AllowOverride None
Require all granted
Options Indexes FollowSymLinks
AllowOverride None
Require all granted
Require all denied
基本的に拒否の設定になっているので、/etc/apache2/sites-available/000-default.conf に個別設定する必要がある。
...
Require all granted
....
Ubuntuのユーザ関連のコマンドは、Debianと異なるようだ。
rootログイン
$ sudo su -sudo権限
sudo権限もつけておく
$ sudo gpasswd -a xxx sudo
タミヤから発売された、マイコンロボット工作セット (クローラータイプ)を購入して、Macに接続してみました。
作成してみる
プラモデル作りなんて小学生以来ですが、接着剤とか塗料とかなくても部品を組み立てるだけです。
プログラムが苦手な人でも作れますが、小学生が作るのはちょっと大変かも知れません。 ギヤーの作成がちょっと面倒くさい
mirco:bit の基盤
mirco:bit の超音波センサー
完成
Mac Book Pro と micro:bit をケーブルを接続
Mac Book Pro と micro:bit をケーブルを接続するには、USB Type-C と Mirco USBケーブルを利用して接続します。
Macに接続して認識できました。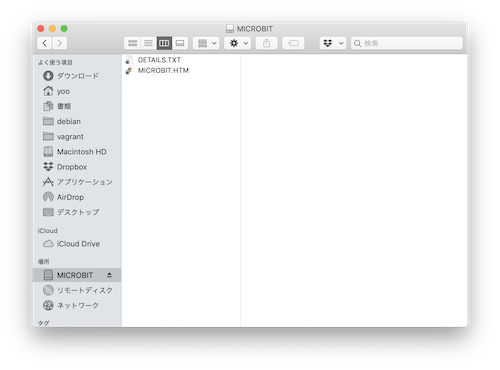 
ターミナル上で確認すると「cu.usbmodemxxxxx」として認識されています。
コントローラを用意
micro:bit を別途購入することでロボットを外部コントロールする事も可能です。
別途、micro:bit とその電源として電池ボックスセットも購入
BBC Micro Bit (マイクロ：ビット) 保護ケースアクリル透明ケースおよびAAA電池バッテリボックスmicro bitボード電源コネクタとの互換性BBC micro bitボード
サンプルプログラミングをインストール
Macに接続したら、タミヤから用紙されているプログラミング（.hexファイル）をMICROBITドライブにインストールして確認します。
（インストール後は、USBケーブルを抜いて主電源で動作確認）
・BBC マイクロビットのプログラムについて
・マイコンロボット工作 プログラミング Q&A
・出荷時のプログラム https://www.tamiya.com/cms/img/usr/item/7/71201/01_DrivingProgram_v1.hex
カスタムプログラミングは、「MakeCode for micro:bit」で行います。
pgAdmin4 からブラウザで起動することになった。
ただポートを自動生成してブラウザ起動するので、ブラウザを閉じてURL（ポート）がわからないと開けないという仕様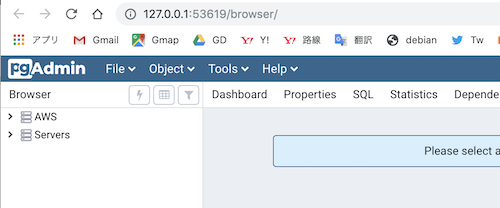 
pgAdmin4アプリ自体をクリックしても開かないので以下で対応 - pgAdmin4 メニューのURLコピー - pgAdmin4 シャットダウン
pgAdmin4 メニューのURLコピー
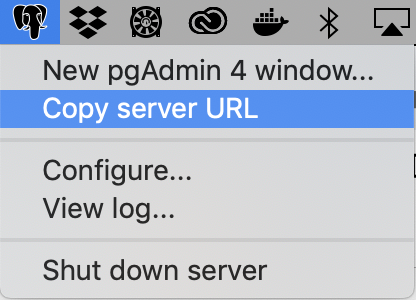コピー後にブラウザでアクセス
pgAdmin4 シャットダウン
それでもひらけない場合は、シャットダウンして再起動 
2019/9時点、MacOSX でAndroid 開発する場合、Java 8 が必要 ライセンスの関係上 Oracleにユーザ登録する必要があるが、Homebrew でオープン系でJava8構築することも可能
homebrew-cask-versions で Java8インストール
caskインストール
$ brew tap homebrew/cask-versions
caskで adoptopenjdk8 corretto8 zulu8インストール
$ brew tap homebrew/cask-versions
$ brew cask install adoptopenjdk8
$ brew cask install corretto8
$ brew cask install zulu8
jEnv
Java のバージョンを複数管理したい場合は jEnvを利用する *Android開発だけならば必要はない
$ git clone https://github.com/gcuisinier/jenv.git ~/.jenv
.bash_profile（.bashrc）設定
.bash_profileもしくは .bashrc に環境変数を設定
export PATH="$HOME/.jenv/bin:$PATH"
eval "$(jenv init -)"
jEnvバージョン確認
$ jenv versions
* system (set by /Users/yoo/.jenv/version)
Java情報確認
$ /usr/libexec/java_home -V
Matching Java Virtual Machines (1):
1.8.0_221, x86_64: "Java SE 8" /Library/Java/JavaVirtualMachines/jdk1.8.0_221.jdk/Contents/Home
/Library/Java/JavaVirtualMachines/jdk1.8.0_221.jdk/Contents/Home
項目
- Xcode
- JavaSDK8
- gradle
- Kotlin
- Android Studio
Xcodeインストール
もろもろツールをインストールするためにXcodeをインストールして起動済みにしておく
Java SDK8のインストール
2019/09/25時点でライセンスの関係上、Oracleからインストーラをダウンロードするか、Homebrew と cask でインストールすることになる。
Oracle JDK8インストーラー
Java SE Downloadsからインストールする場合にユーザ登録が必要
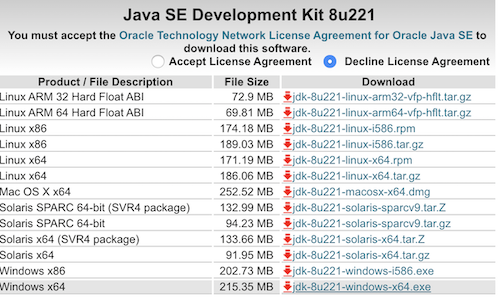
homebrew-cask-versions で Java8インストール
インストーラを利用せず、Homebrew で構築することも可能 Java8 を HomebrewとjEnvで構築
SDKバージョン切り替え
Gradleインストール
Gradle は オープンソースのビルドシステム Android Studio を利用するときに便利
SDKMANのインストール
SDKMANバージョン確認
gradleインストール
gradle バージョン確認
<
h2 class="h2">Kotlinインストール
Kotlin バージョン確認
利用SDKの確認
Android Studioインストール
AVD(Android Virtual Device)
AVD Manager から仮装端末をインストール
SDK Manager
SDK Manager で不足しているツールをインストールする
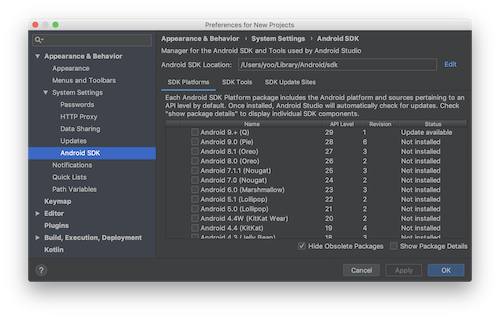
Android SDK Platforms
SDK Platforms で利用したい Android OSバージョンをインストール
Android SDK Tools
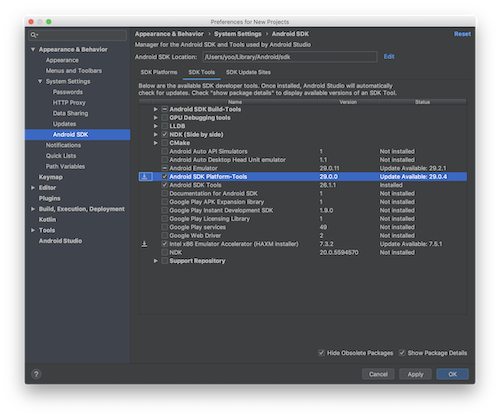
- Android SDK Build-Tools 28
- Android Emulator
- Android SDK Platform-Tools
- Android SDK Tools
- Intel x86 Emulator Accelerator(HAMX instraller)
- NDK
Android SDK Platform Tools
Android SDK Tools
Android 9.0 の場合 - Android SDK Platform 28 - Sources For Android 28 - Google APIs Intel x86 Atom_64 System Image
Android NDK
Mac OSX 設定
.bash_profileに環境変数設定
adb確認
文字コードを en_US.UTF-8 から ja_JP.UTF-8 に変更する方法
※この処理は DBが全てリセットされてしまうので注意！
# localedef -i ja_JP -c -f UTF-8 -A /usr/share/locale/locale.alias ja_JP.UTF-8 # vi /etc/locale.gen ja_JP.UTF-8 UTF-8 # update-locale LANG=ja_JP.UTF-8
再ログイン
# locale LANG=ja_JP.UTF-8 LANGUAGE= LC_CTYPE="ja_JP.UTF-8" LC_NUMERIC="ja_JP.UTF-8" LC_TIME="ja_JP.UTF-8" LC_COLLATE="ja_JP.UTF-8" LC_MONETARY="ja_JP.UTF-8" LC_MESSAGES="ja_JP.UTF-8" LC_PAPER="ja_JP.UTF-8" LC_NAME="ja_JP.UTF-8" LC_ADDRESS="ja_JP.UTF-8" LC_TELEPHONE="ja_JP.UTF-8" LC_MEASUREMENT="ja_JP.UTF-8" LC_IDENTIFICATION="ja_JP.UTF-8" LC_ALL=
PostgreSLQ 停止 & クラスター削除
# /etc/init.d/postgresql stop # pg_dropcluster --stop 11 main
PostgreSLQ クラスター作成 & 起動
# pg_createcluster 11 -e UTF-8 --locale ja_JP.UTF-8 --start main # /etc/init.d/postgresql start
DB確認
$ psql -l List of databases Name | Owner | Encoding | Collate | Ctype | Access privileges -----------+----------+----------+-------------+-------------+----------------------- postgres | postgres | UTF8 | ja_JP.UTF-8 | ja_JP.UTF-8 | template0 | postgres | UTF8 | ja_JP.UTF-8 | ja_JP.UTF-8 | =c/postgres + | | | | | postgres=CTc/postgres template1 | postgres | UTF8 | ja_JP.UTF-8 | ja_JP.UTF-8 | =c/postgres + | | | | | postgres=CTc/postgres
vagrant で Apache を利用するとパーミッションの問題が発生する 一般ユーザ同様に、グループ設定を行う
Ubuntu
CentOS
AWS の Linux2 は最適化された（？）パッケージが用意されている
- CentOS7
- Apache2
- PHP7.3
- PostgreSQL *コマンドは sudo でなく root で実行している（root パスワードを別途設定済み）
yum アップデート
# yum update -y
Apache2
Apache インストール
# yum -y install httpd
サービス起動
# systemctl start httpd
*CentOS6系では chkconfig httpd on
自動起動設定
# systemctl enable httpd.service
Created symlink from /etc/systemd/system/multi-user.target.wants/httpd.service to /usr/lib/systemd/system/httpd.service.
自動起動設定確認
# systemctl is-enabled httpd
ec2-user 設定
/var/www/ を ec2-user が利用できるように設定する
ec2-user を apache に追加
# usermod -a -G apache ec2-user
/var/www の権限
デフォルトの DocumentRoot である /var/www の権限を ec2-user : apache に変更 ディレクトリ(775)とファイル(664) で利用できるようにする
# chown -R ec2-user:apache /var/www
# chmod 2775 /var/www && find /var/www -type d -exec chmod 2775 {} ;
# find /var/www -type f -exec chmod 0664 {} ;
*2775 の 2 は setgid
ec2-user で所属グループの確認
ec2-user を再ログインして確認
$ groups ec2-user
PHP7.3
Amazon Linux2 用にパッケージが用意されており、PHP7.3 はここからインストールする。
Amazon Linux2 専用のパッケージ確認
# amazon-linux-extras list
.....
# amazon-linux-extras info php7.3
インストール
# amazon-linux-extras install php7.3
amazon-linux-extras で足りないパッケージは、yum でインストールすると良い
Composer インストール
$ curl -sS https://getcomposer.org/installer | php
All settings correct for using Composer Downloading...
Composer (version 1.9.0) successfully installed to: /home/vagrant/composer.phar
Use it: php composer.phar
/user/local/bin に移動
$ sudo mv bin/composer /usr/local/bin/composer
composer初期化
$ composer init
composer.json が作成される
composer install
$ composer install
Loading composer repositories with package information Updating dependencies (including require-dev) Nothing to install or update Generating autoload files
PostgreSQL10
amazon-linux-extras
amazon-linux-extras では psql コマンドのみのインストールの模様
# amazon-linux-extras install postgresql10
yum インストール
# yum install -y postgresql-server postgresql-devel postgresql-contrib
サービス起動
# systemctl start postgresql # postgresql-setup initdb
自動起動設定
# systemctl enable postgresql.service
postgres ユーザで確認
# su - postgres
$ psql -l
could not change directory to "/home/ec2-user": Permission denied List of databases
.....
外部からのアクセス設定
パスワードで制御するかIPで制御するか、はたまたその他の方式かはセキュリティポリシーによって違うので割愛 （postgres.conf & pg_hba.conf 設定など）
AWS はセキュリティグループで PostgreSQLのポート設定しないと一切アクセスできない。
AWS セキュリティグループ
セキュリティグループ > EC2 に紐付いたグループ > インバウンド > 編集
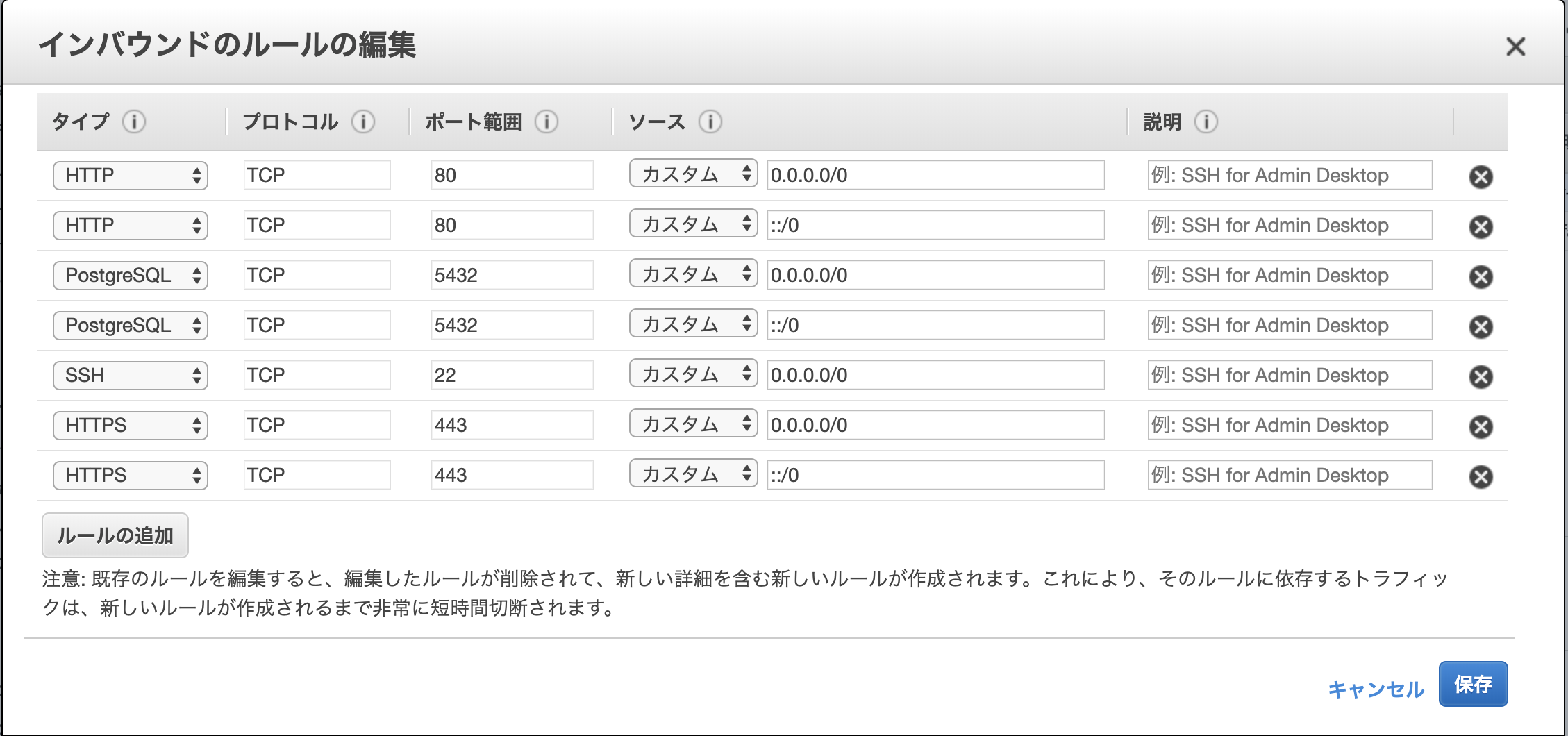
上記の設定は 5432 に全ての IPを許可（CIDR形式）しているので、必要であれば IP制限する
（postgresパスワードや、pg_hba.conf で制限しても良い）
Python単体 と Anaconda は比較的衝突しやすいので、Anacondaを削除してみる
anaconda-clean のインストールと実行
$ conda install anaconda-clean
$ anaconda-clean
anaconda_backup の削除
$ rm -rf ~/.anaconda_backup
<
h2 class="h2">anaconda 本体の削除 環境によってパスが異なるが、which anaconda などでパスを確認して削除
$ cd ~/.pyenv
$ rm -rf versions
$ cd .pyenv/shims
$ rm -rf anaconda*
<
h2 class="h2">.bash_profile から環境変数の削除 ~/.bash_profile に環境変数が追加されていた場合はこれを削除
ターミナルを再起動すると anaconda は動作しない
